1. 什么情况下能用NA准确估算光纤接收角？

多模光纤的最大接收角可通过数值孔径(NA)比较准确地估算，但是这种关系对单模光纤不适用。

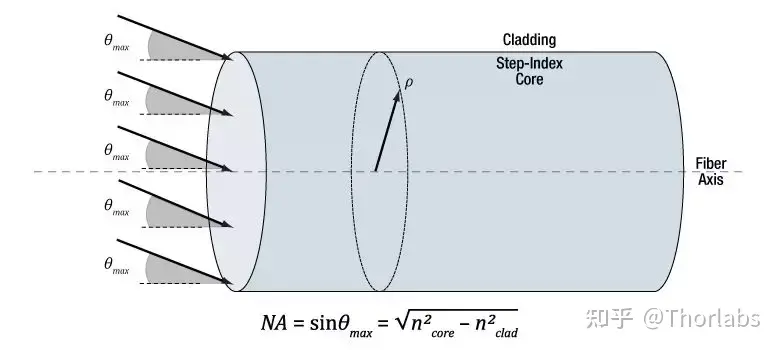
NA和最大接收角( ${\theta }_{max}$ )的关系可通过几何光学计算得到，公式请见下图。如果把入射光看成一条条射线， ${\theta }_{max}$ 就表示光纤收集离轴光线的能力：入射角小于等于 ${\theta }_{max}$ 的光线(红色和粉色)在纤芯和包层界面发生全内反射(TIR)，将被约束在纤芯中向前传播；入射角大于 ${\theta }_{max}$ 的光线(蓝色)由于折射最终被损耗。

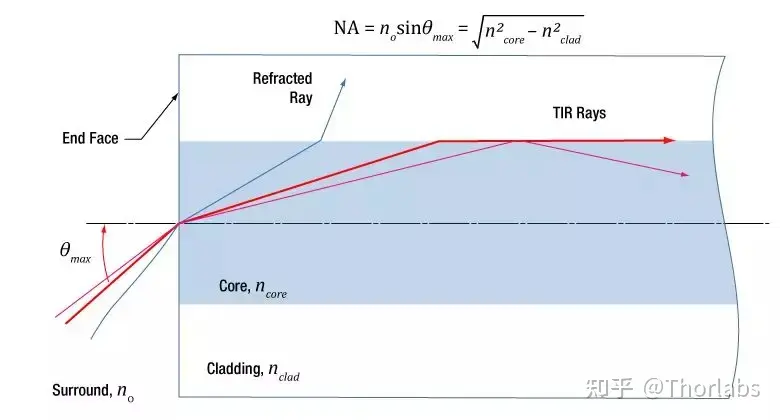
入射角和光纤模式

入射角 $\le {\theta }_{max}$ 的光线将被耦合到多模光纤某个导模中。一般而言，入射角越小，被激发的光纤模式阶数越低。大部分能量集中在中心附近的低阶模式中，正入射光线激发最低阶模式。下面是两种多模光纤传播示意图。

单模光纤不一样

使用上述公式计算的NA不是单模光纤的最大入射角，故无法表征单模光纤的光接收能力。单模光纤中只存在由0度入射光激发的最低阶导模，传播示意图如下。

使用NA估算单模光纤输出的发散角很不准确。此时光束因衍射而发散，几何光学不考虑这种效应，所以需要使用波动光学。如何使用高斯光束传播理论计算单模光纤的发散角请看第3部分。

2. 为什么MFD是单模光纤耦合的重要参数？

光束沿单模光纤传播时维持接近高斯形的强度轮廓，可用模场直径(MFD)表征轮廓宽度，即强度降到峰值的1/e²时所跨的宽度。经验法则：单模光纤的MFD约为纤芯直径的1.15倍。

入射光越接近高斯光，耦合效率越高。如果入射光为高斯光，并且束腰等于光纤MFD，那么可以达到很高的耦合效率。在高斯光束公式中用MFD代入束腰直径可以准确计算单模光纤的耦合参数和发散角。

确定耦合参数

单模光纤只有一种导模，可用贝塞尔函数描述。由于形状相似，使用高斯函数可以简化光纤模式，同时提供准确结果。下图中展示了单模光纤的模式强度轮廓，入射光只有与之匹配才能被耦合到导模中。

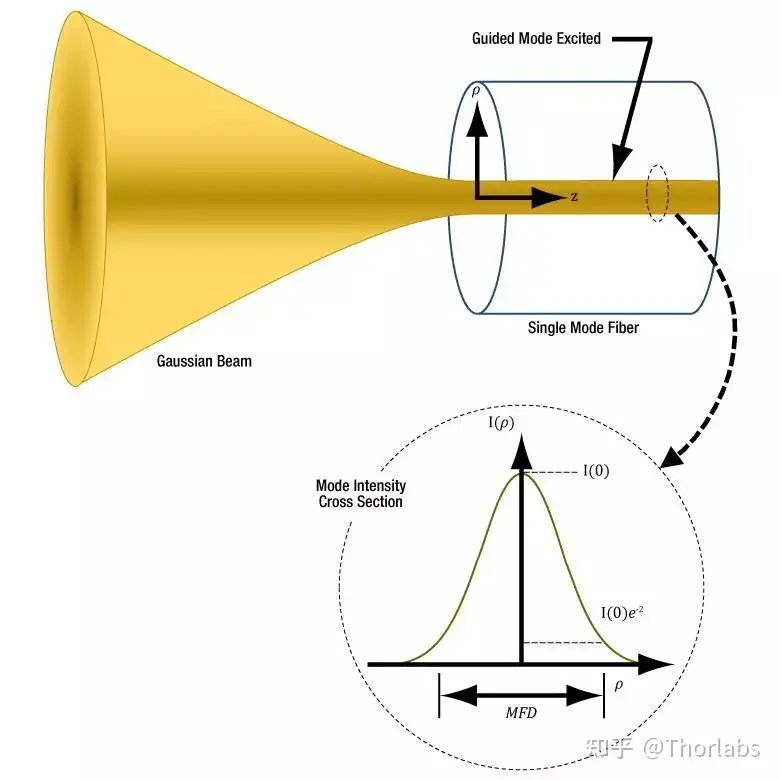
单模光纤耦合

提高单模光纤耦合效率要求入射高斯光束的束腰位于光纤端面，且束腰强度和模式强度匹配重合。如果束腰直径不等于MFD、光束强度轮廓变化或者偏离，又或者没有沿光纤轴向入射，这些情况都会降低耦合效率。详细介绍请见第4部分。

3. NA能否准确估算单模光纤输出的发散角？

使用NA估算单模光纤的发散角存在较大误差，更准确的方法是使用高斯光束传播理论。单模光纤的远场发散角的近似计算公式如下，其结果是以弧度为单位的发散角或接收角。

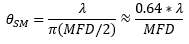
单模光纤的输出类似高斯光，如用几何光学计算发散角有较大偏差。几何光学计算的发散角等于arcsin(NA)，只适用于一般的多模光纤。

单模光纤输出高斯光束，瑞利距离和z点处的光束半径分别用下面两个公式计算。

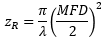
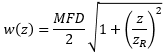
据此可以准确模拟单模光纤输出光束的发散角，如下图所示。从图中可以看出，根据几何光学理论使用NA计算发散角存在很大误差。此例中NA和MFD分别等于0.13和6.4 µm。工作波长为980 nm，瑞利距离为32.8 µm。

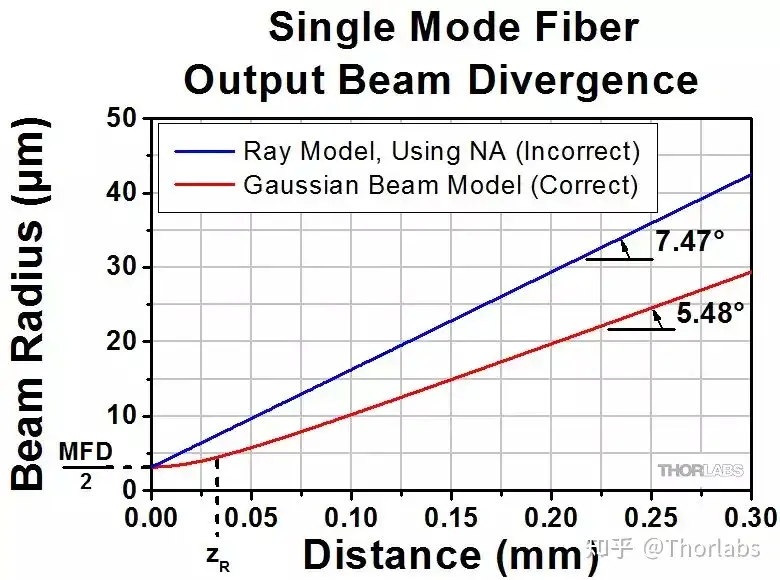
从图中可看出，在瑞利距离以内时，光束发散率不是线性的，而在远场可看成近似线性。图中标注的两个角度值根据各自曲线的斜率计算。如果使用上面的远场近似公式计算，结果转换成角度为5.61°，误差较小。

4. 影响单模光纤耦合效率的因素有哪些？

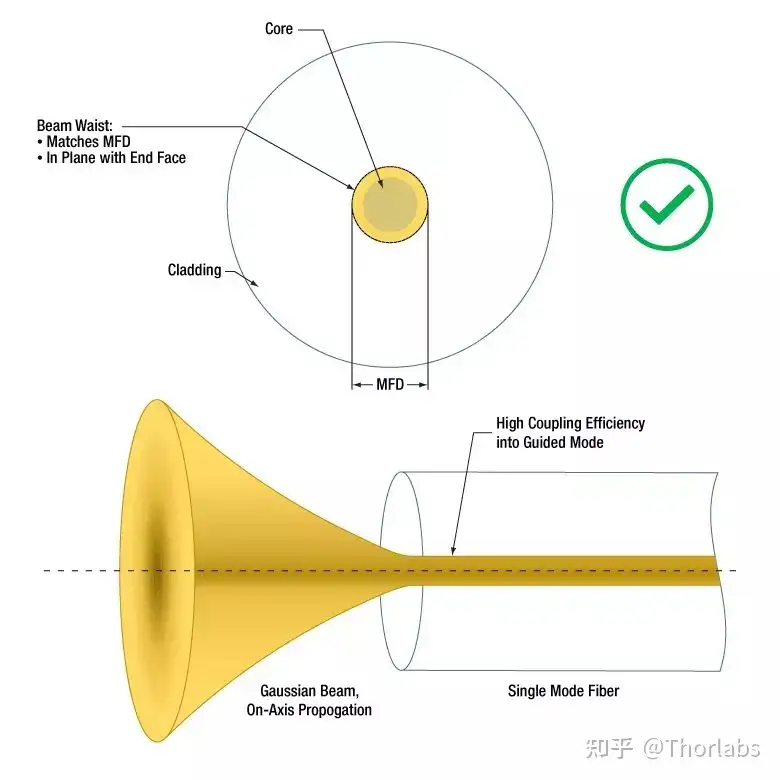
调节入射光束的角度、位置和强度轮廓可以提高单模光纤的耦合效率。假设光纤端面为平面并与轴向垂直，满足以下条件的光束可以到达最高耦合效率：

• 高斯强度轮廓

• 从光纤端面正入射

• 束腰位于光纤端面

• 束腰中心对准纤芯中心

• 束腰直径等于光纤MFD

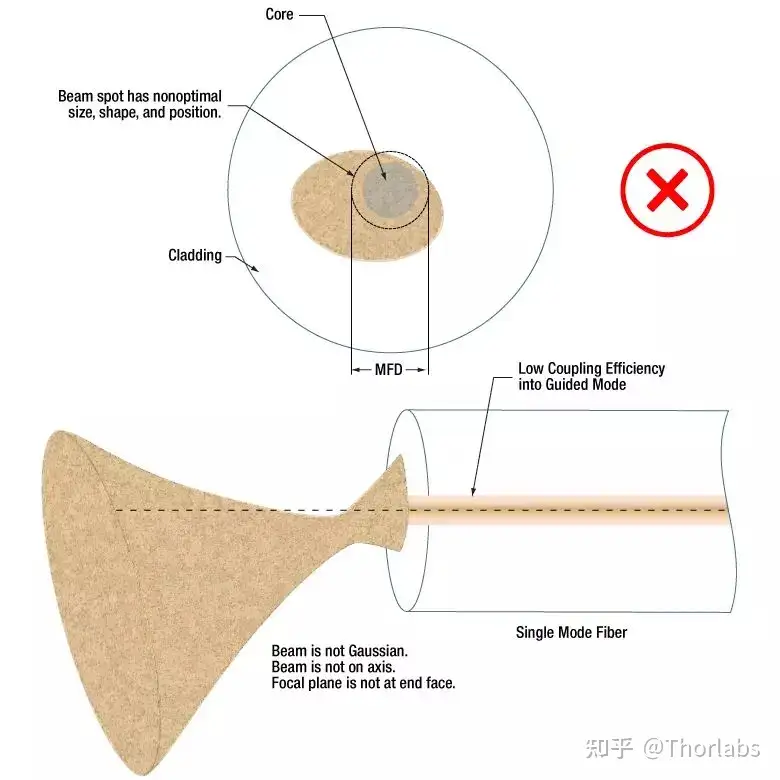
光源可能限制耦合效率

如果激光器只发射最低阶横模，那么输出近似高斯光束，可以高效耦合到单模光纤中。但是多模激光或宽带光源和单模光纤的耦合效率很低，即使聚焦到纤芯区域，大部分光会被泄露。这是因为多模光源只有一部分光匹配单模光纤导模特征，所以多模光源可以用多模光纤提供更高的耦合效率。

5. 多模光纤的最大接收角是不是固定的？

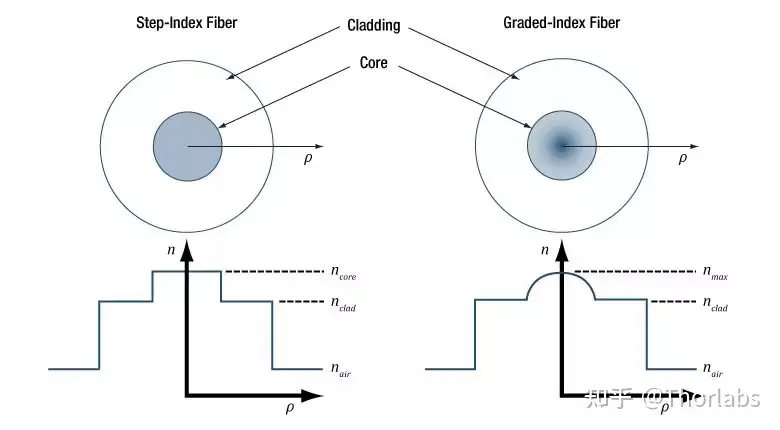
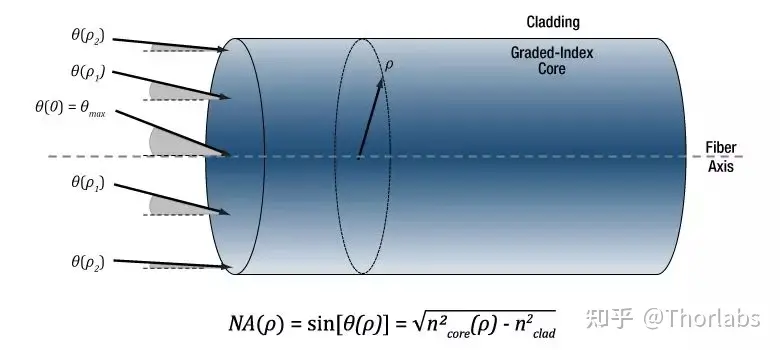
这个问题取决于光纤类型。对于阶跃折射率多模光纤，纤芯上每个点的最大接收角都是一样的。但是，渐变折射率多模光纤只有纤芯中心处才能提供最大的入射角。距离中心越远，最大接收角越小，在包层界面附近的最大接收角趋近于0。

下图中比较了两种多模光纤的不同：左边为阶跃折射率多模光纤，折射率在整个纤芯上都是恒定的。右边为渐变折射率多模光纤，折射率随纤芯位置不同，最大折射率一般在中心位置。

对于阶跃折射率多模光纤，如果入射光线角度小于等于|θmax|，就能被阶跃折射率多模光纤高效耦合。纤芯径向上每个点的最大接收角都是一样的，详见下图。

对于渐变折射率多模光纤，因为纤芯折射率随径向距离变化，所以接收角也随径向距离变化。纤芯中心处的接收角最大，而包层边界附近的接收角趋近于零，详见下图。

阶跃折射率还是渐变折射率？

阶跃折射率多模光纤能接收更多的光。渐变折射率多模光纤中所有导模具有相似的传播速度，可以降低光束传播过程中的模式色散。

如果应用中要求在多模光纤中耦合尽可能多的光，并且受模式色散影响较小，阶跃折射率多模光纤可能是更好的选择。反之应该考虑渐变折射率多模光纤。